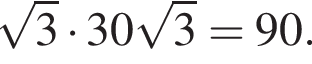Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Внутренний угол правильного многоугольника равен 135°. Выберите все верные утверждения для данного многоугольника.
1. Многоугольник является восьмиугольником.
2. В многоугольнике 40 диагоналей.
3. Если сторона многоугольника равна 2, то радиус вписанной окружности равен 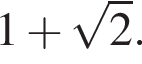
4. Площадь многоугольника со стороной a можно вычислить по формуле 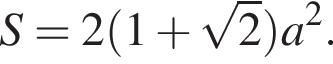
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Если BC — диаметр, O — центр окружности,
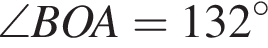 (см. рис.), то градусная мера вписанного угла BCA равна:
(см. рис.), то градусная мера вписанного угла BCA равна:
Если вписанный угол KML изображенный на рисунке, равен 38°, то вписанный угол KNL равен:
На одной стороне прямого угла О отмечены две точки А и В так, что ОА = 1,7, OB = а, ОА < ОВ. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки А, В и касающейся другой стороны угла.
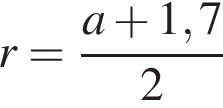
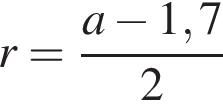
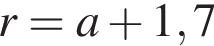
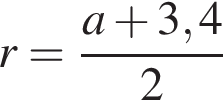
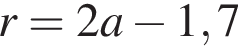
На рисунке изображены две окружности с центрами в точках A и B. Если MK = 48, то сумма радиусов этих двух окружностей равна:
Две окружности с центрами A и B касаются в точке M. Найдите длину отрезка CN, если
 и диаметр большей окружности на 25 больше радиуса меньшей окружности.
и диаметр большей окружности на 25 больше радиуса меньшей окружности.
ABCD — прямоугольник. Точка N — середина стороны ВС. Отрезок DN пересекает диагональ АС в точке О (см. рис.). Найдите площадь четырехугольника ONBA, если площадь прямоугольника ABCD равна 492.
Прямая, проходящая через вершину К треугольника KMN, делит его медиану MA в отношении 8 : 3, считая от вершины M, и пересекает сторону MN в точке B. Найдите площадь треугольника KMN, если площадь треугольника KMB равна 16.
Основание остроугольного равнобедренного треугольника равно 10, а синус противоположного основанию угла равен 0,6. Найдите площадь треугольника.
Площадь круга равна ![]() Диаметр этого круга равен:
Диаметр этого круга равен:
Из точки А проведены к окружности радиусом ![]() касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
В прямоугольном треугольнике ACB
 CH и CK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ACB, если CK = 8,
CH и CK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ACB, если CK = 8, 
Прямоугольный треугольник, длина гипотенузы которого равна 10, высота, проведенная к ней, равна 3, вращается вокруг прямой, перпендикулярной гипотенузе и проходящей в плоскости треугольника через вершину большего острого угла. Найдите объем V тела вращения и в ответ запишите значение выражения ![]()
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 4, BC = ![]()
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Отрезок AB пересекает плоскость α в точке O. Точка M делит отрезок AB в отношении 3 : 2, считая от точки А. Из точек А, В, M проведены параллельные прямые, пересекающие плоскость α в точках A1, B1, M1 соответственно. Найдите длину отрезка ММ1, если 
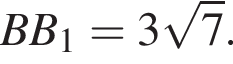
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
На рисунке две прямые пересекаются в точке О. Если
 то угол BOC равен:
то угол BOC равен:
На рисунке a || b, 
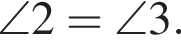 Найдите градусную меру угла 4.
Найдите градусную меру угла 4.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Из точки A к окружности с центром O проведены две касательные AB и AC, где B и C — точки касания. Через точки C и O проведена прямая, которая пересекает касательную AB в точке M (см. рис.). Найдите градусную меру угла 1, если ∠AMC = 44°.
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите значение выражения 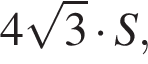 где S — площадь трапеции, если большее основание трапеции равно
где S — площадь трапеции, если большее основание трапеции равно ![]() а один из углов трапеции равен 60°.
а один из углов трапеции равен 60°.
Дан параллелограмм ABCD, 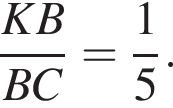 Отрезок DK пересекает сторону АВ в
Отрезок DK пересекает сторону АВ в
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен ![]() Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Четырёхугольник ABCD вписан в окружность. Если 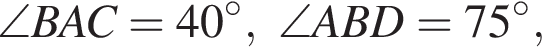 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Длины сторон параллелограмма относятся как 4 : 5, а высота, проведенная к большей стороне, равна 6. Найдите значение выражения ![]() где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.
где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.

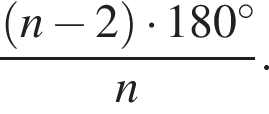 Тогда
Тогда 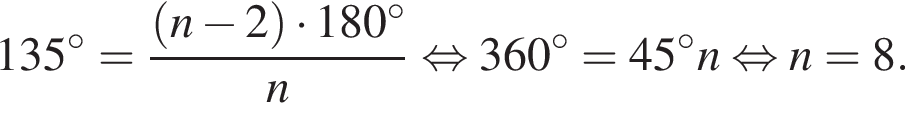
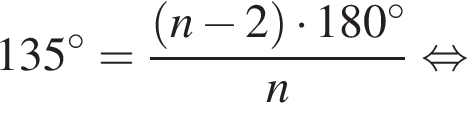
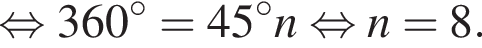
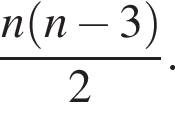 При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.
При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.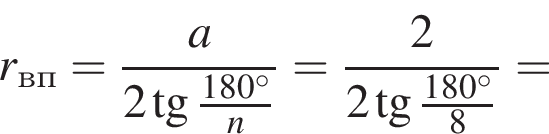
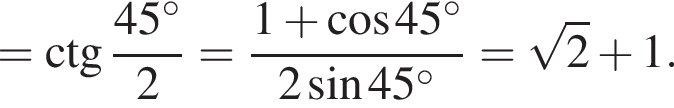
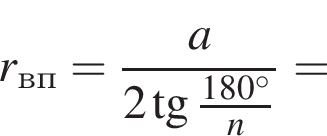
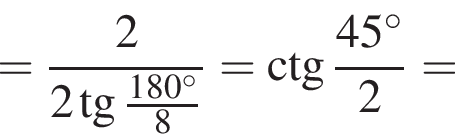
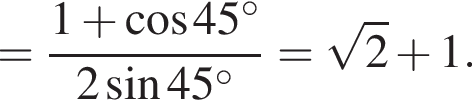
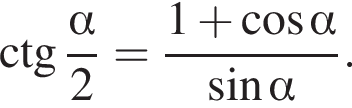
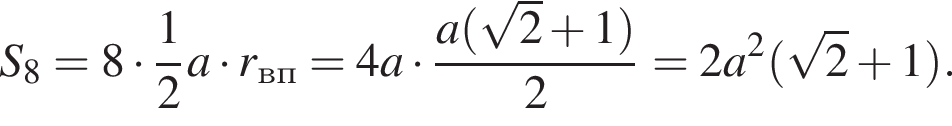
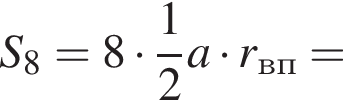
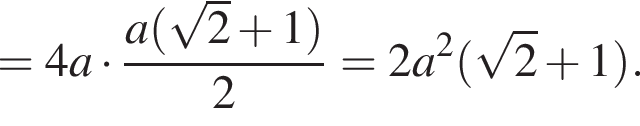
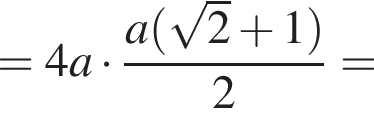
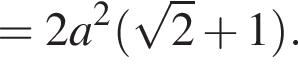
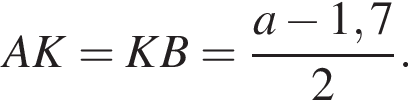
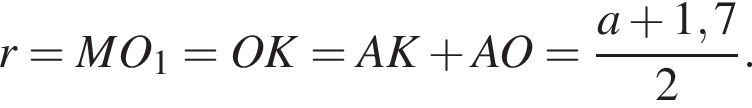
 Значит, длина отрезка
Значит, длина отрезка 
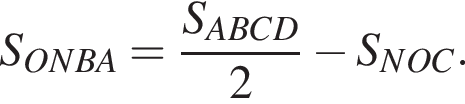 Треугольники ONC и AOD подобны по двум углам. Тогда
Треугольники ONC и AOD подобны по двум углам. Тогда 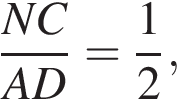 отношение площадей подобных треугольников равно квадрату коэффициента подобия, поэтому
отношение площадей подобных треугольников равно квадрату коэффициента подобия, поэтому 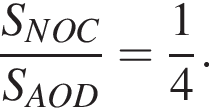 Отношение
Отношение 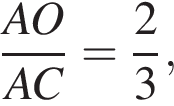 тогда
тогда 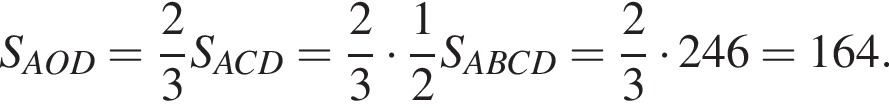
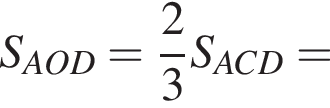
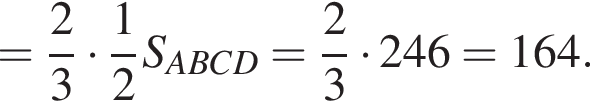
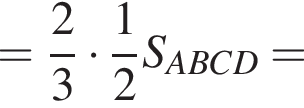
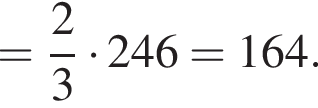
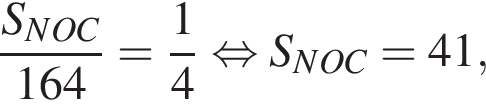 то
то 
 По теореме о пропорциональных отрезках получаем, что
По теореме о пропорциональных отрезках получаем, что 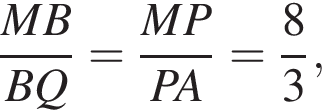
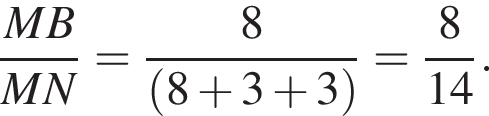
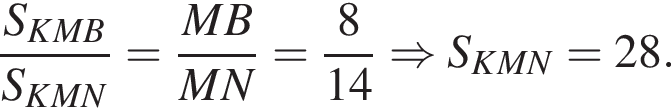
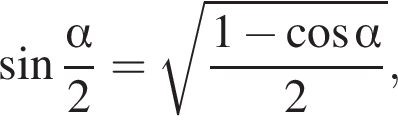 где
где 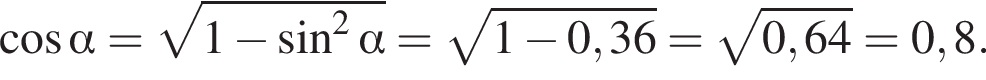
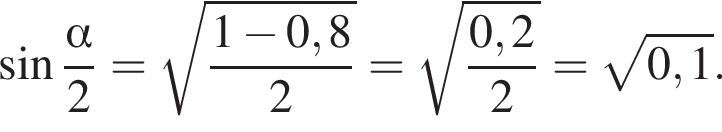
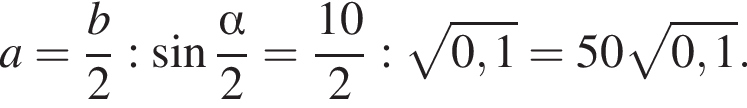 Тогда площадь треугольника равна:
Тогда площадь треугольника равна: 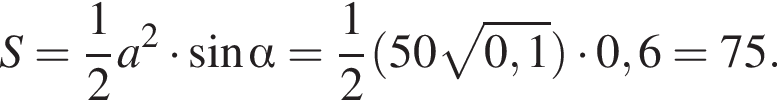
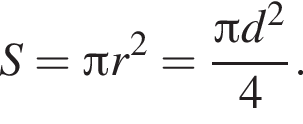 Следовательно,
Следовательно, 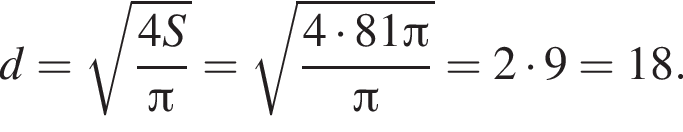
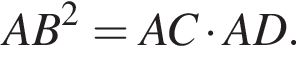 Обозначим AB за x, тогда
Обозначим AB за x, тогда  Тогда:
Тогда: 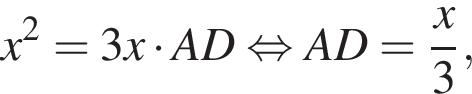 при этом
при этом 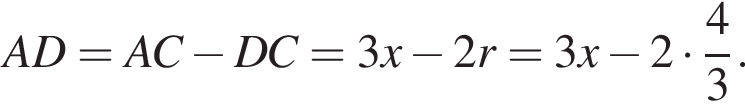 Получим:
Получим: 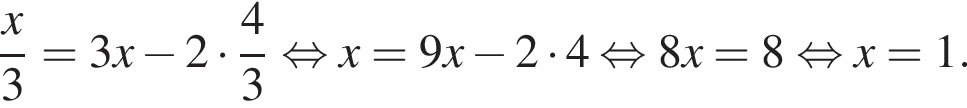
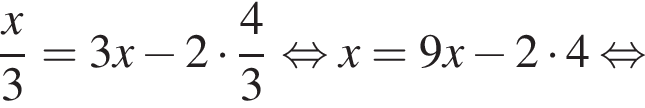
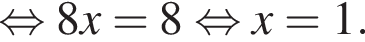
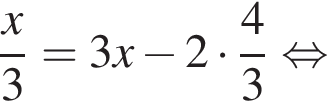
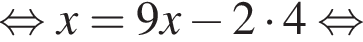
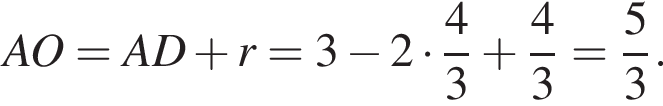
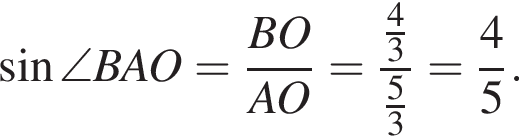 Тогда площадь треугольника ABC:
Тогда площадь треугольника ABC: 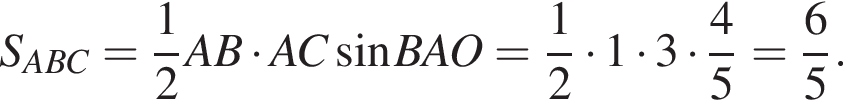
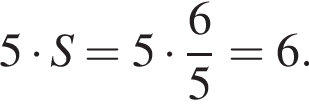
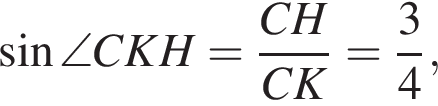 а CK = 8, получаем, что CH = 6. Отрезок CK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина CK равна половине длины гипотенузы, тогда длина гипотенузы равна 2CK = 16. Площадь треугольника ACB равна
а CK = 8, получаем, что CH = 6. Отрезок CK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина CK равна половине длины гипотенузы, тогда длина гипотенузы равна 2CK = 16. Площадь треугольника ACB равна 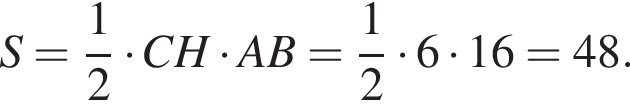
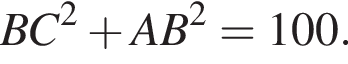 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: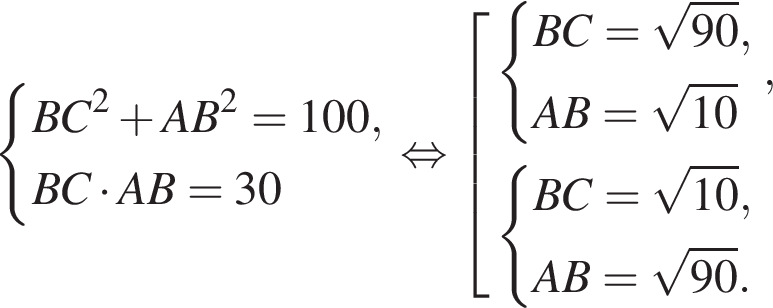
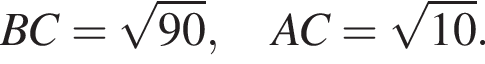 По теореме Пифагора найдем
По теореме Пифагора найдем 
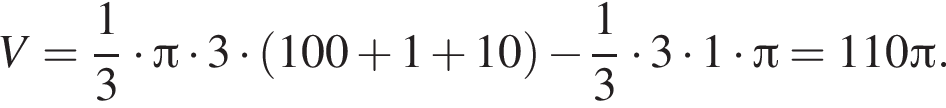
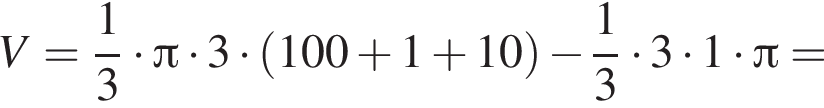
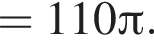
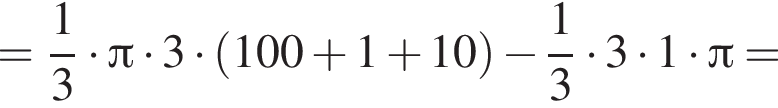
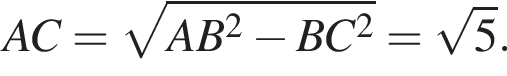 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC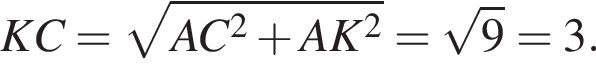

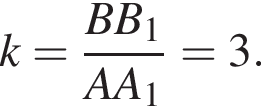 Известно, что
Известно, что 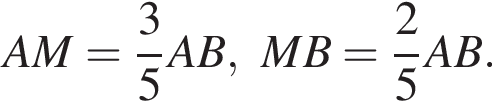 Тогда
Тогда 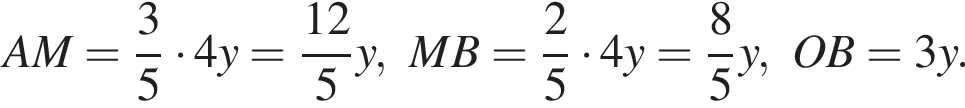
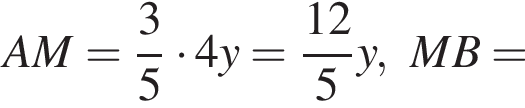
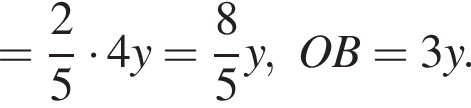
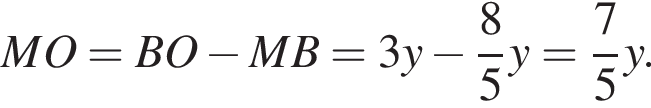 Из подобия треугольников имеем:
Из подобия треугольников имеем: 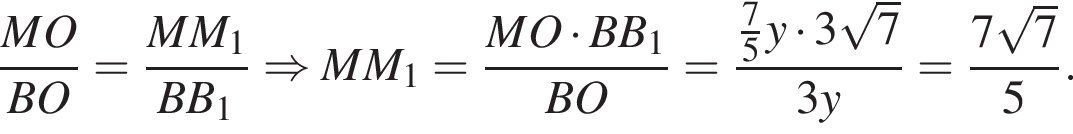
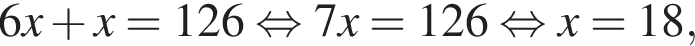
 равна 360°, поэтому
равна 360°, поэтому 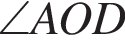 равен 60°. Углы
равен 60°. Углы 
 Значит,
Значит, 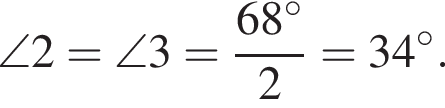 Тогда и
Тогда и 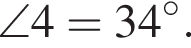
 равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.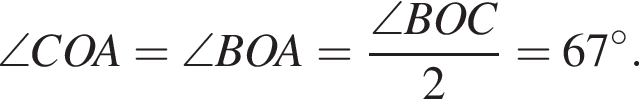
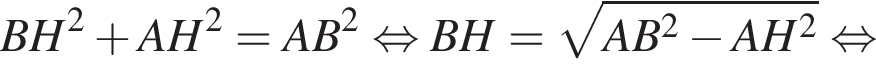
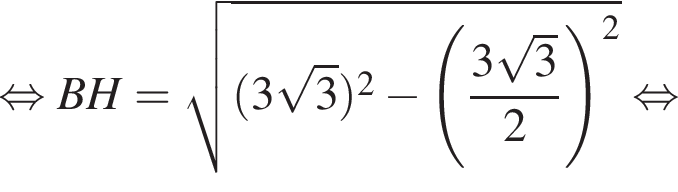
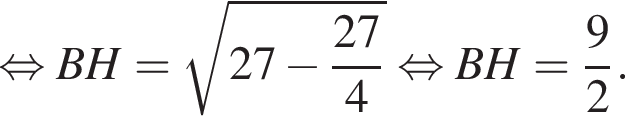
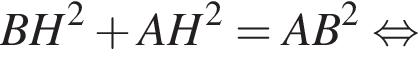

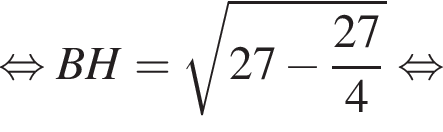
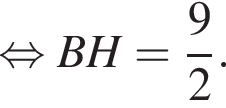
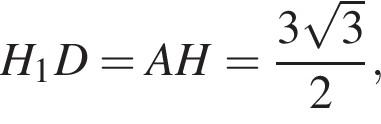 тогда
тогда 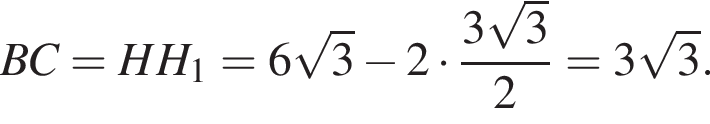
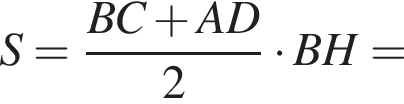
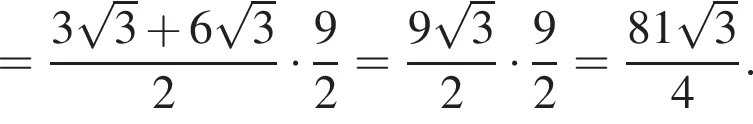
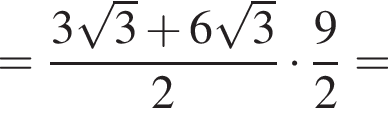
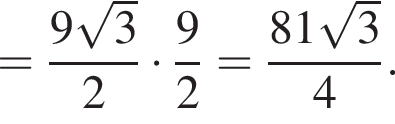
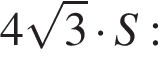
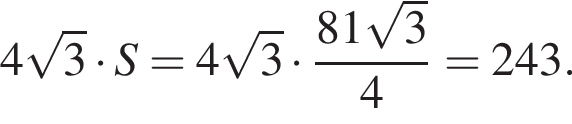
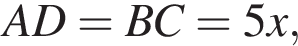 тогда
тогда  и
и 
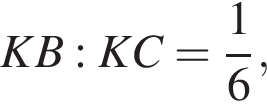 поэтому
поэтому 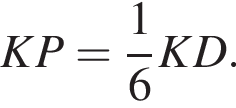
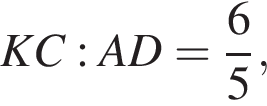 поэтому
поэтому 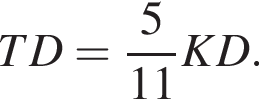
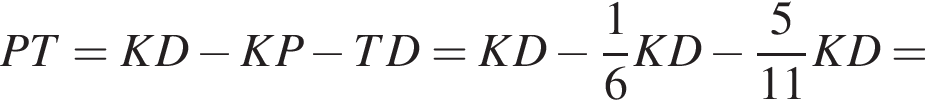
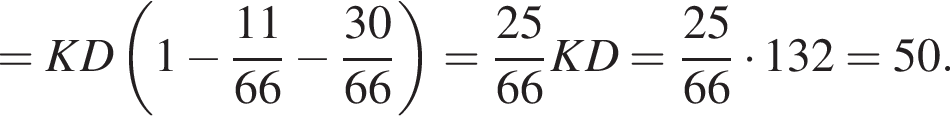
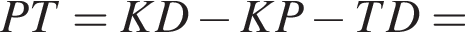
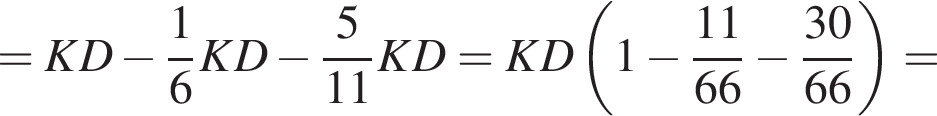
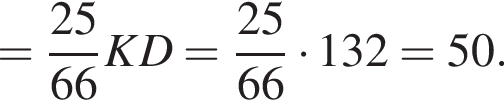
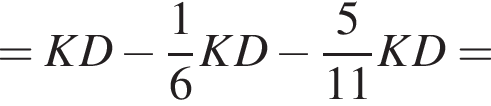
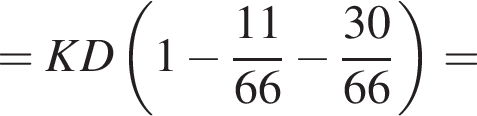
 Поскольку все стороны трапеции, кроме большего основания равны a, получим
Поскольку все стороны трапеции, кроме большего основания равны a, получим  Тогда
Тогда 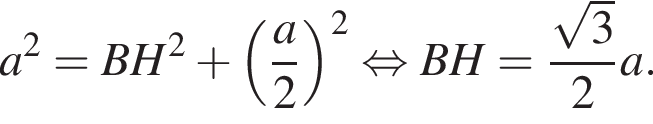

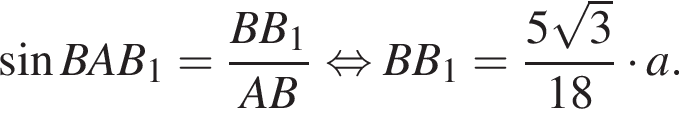
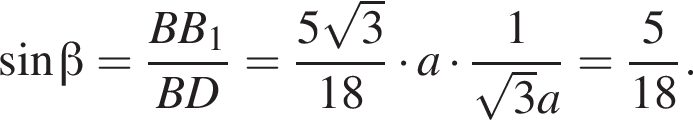
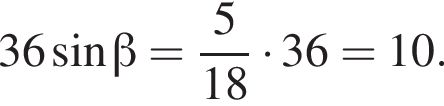


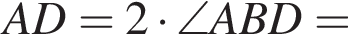

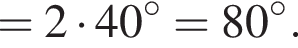
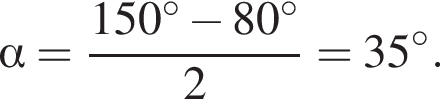
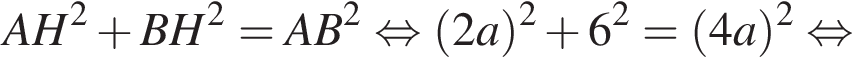
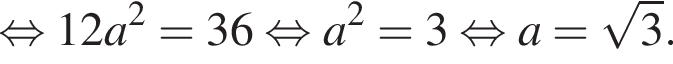
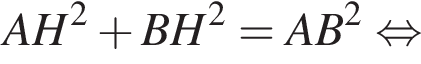
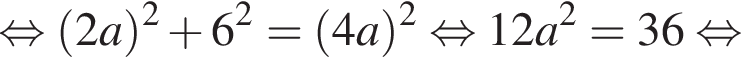

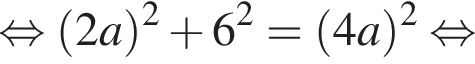
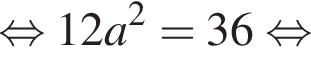
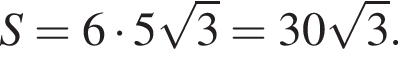 Значение выражения
Значение выражения